Special thanks to my friends Quentin and Jai for reviewing the draft versions of this piece.
Charity Sweet Jars
Late on a Friday afternoon at work, two colleagues appeared at my desk brandishing charity donation boxes and a jar brimming with sweets. A game was afoot! Specifically, “guess the number of sweets in a jar”, in aid of Macmillan Cancer Support.
Delighted, I examined the jar. But as I formulated my guess, it struck me that my colleagues had inadvertently presented the makings of a crude experiment. I was one of the final desk stops on their fundraising crusade, so they had already collected several dozen independent guesses. This reminded me of the "wisdom of crowds" effect. This effect describes how collective estimates often converge remarkably close to the true value, despite significant individual variations, and can solve problems better than most individuals within the group, including experts.
My request to base a guess on the mean of previous responses was (quite reasonably) declined, but my curiosity was piqued and the colleagues agreed to share a complete dataset once the competition results were announced.
Using this data, I investigated the following hypothesis: "A measure of central tendency derived from participants' guesses will be closer to the true number of sweets in the jar (in terms of absolute error) than the majority of individual guesses."
Materials & Methods
Two jars were circulated in different sections of an open-plan office environment during normal working hours (14:00-16:30 GMT). Participants made individual guesses in isolation. The fundraisers collected 23 guesses for Jar A and 44 guesses for Jar B. Jar A contained 110 items and Jar B contained 120 items.
Given that this test is rudimentary in nature, being the result of happenstance rather than a carefully designed scientific experiment, it is worth highlighting several conditions that are likely to have enhanced or limited the reliability of any findings.
For instance, the following conditions may have improved the generalisability and reduced the error involved in this analysis:
Incentive structure: There was a meaningful financial barrier (£5 minimum entry fee) and a dual-reward mechanism (winning the sweet jar and having a charitable impact). This likely promoted authentic participant engagement as the entry requirement screened out casual participants and the two-part reward system balanced self-interest with prosocial motivation, though this may have attracted participants with particular psychological profiles rather than a representative sample.
Information independence: Participants submitted their estimates in isolation from one another, which prevented direct information cascades and minimised the risk of conformity bias influencing individual judgements. However, it is possible that information leaked within the office environment through pre-existing communication channels, potentially compromising the true independence of estimates.
Diversity (heterogenous mental models): The office workers who participated in the estimation task brought diverse estimation approaches shaped by their distinct organisational roles, enriching the data through multiple problem-solving perspectives. However, the sample's limitation to white-collar corporate professionals excluded potentially valuable viewpoints from other occupational and socioeconomic groups.
In terms of the experiment’s limitations, several factors likely constrained the generalisability of any findings:
Sample size: Most notably, the small sample size of participants (n=67) reduced the study's statistical power and increased the margin of error. With only 67 participants, the findings are unlikely to represent a broader population, making it difficult to detect subtle effects or draw robust conclusions that could be confidently applied to larger groups.
Selection effects: The study population was inherently skewed by the self-selection of participants who actively chose to donate to charity, potentially introducing systematic bias. These individuals may possess distinct psychological, socioeconomic, or demographic characteristics that differentiate them from the general population, such as higher levels of empathy, greater financial security, or stronger prosocial tendencies.
Number preference bias: In cultures using base-10 counting systems, people tend to round to numbers ending in 0 or 5, an effect also known as "terminal digit preference." The organisers' choice of 110 and 120 as correct answers may have played into this bias. As multiples of 10, those answers were more likely to be guessed than numbers like 113 or 118.
Temporal effects: The data was collected over a short time period and participants might have been experiencing workday-related cognitive load effects (such as a postprandial decrease in cognitive performance, also known as a '“post-lunch dip”).
Environmental and settlement effects: While all estimates were made under consistent lighting conditions, the jar's circulation likely caused compaction through movement, potentially affecting volume assessments over time.
Hypothesis Testing
In terms of the results, here is a table showing the guesses for each jar from largest to smallest, and their distance from the true value:
And here are those same results plotted on a bar chart where 0 = the true value, and the x-axis is the distance from the true value:
For Jar A, guesses ranged from 200 (90 sweets too high) to 69 (41 sweets too low). For Jar B, guesses ranged from 204 (84 sweets too high) to 65 (55 sweets too low). The spread of guesses was slightly larger for Jar B, likely reflecting the larger sample size, (range of 139 sweets) compared to Jar A (range of 131 sweets).
Despite the broad spread of guesses, in the case of each jar, several participants guessed quite close to the true value and one participant guessed the exact correct number.
Turning then to the collective measures. A very quick analysis immediately demonstrates that a measure of average of all the prior guesses was a very good estimate of the true value. For Jar A, where the true value was 110:
Arithmetic mean of 113 overestimated by ~3 sweets or 2.39% error.
Median of 105 underestimated by ~6 sweets or 5.00% error.
Trimmed mean (x̄10%) of 111 marginally overestimated by just ~1 sweet or 0.58% error and was closest to true value. (A “trimmed” mean is where the tails of a distribution of estimates are trimmed and then the arithmetic mean is calculated from the truncated distribution)
For Jar B, where the true value was 120:
Arithmetic mean of 124 overestimated by ~4 sweets or 3.33% error.
Trimmed mean (x̄10%) of 122 overestimated by ~2 sweets or 1.78% error.
Median was almost spot on 120 sweets or 0.42% error.
By contrast, on average, any individual guess was significantly further away from the true value.
This can be demonstrated using two statistical measures. Firstly, the mean absolute error (MAE), stated in the same units as the original data (number of sweets), calculates the number of sweets that individual guesses missed the true value by on average. For Jar A, MAE was 23.3. This means that, on average, guesses were off by ~23 sweets. For Jar B, MAE was 30.2, meaning on average, guesses were off by about ~30 sweets. Second, the root mean square error (RMSE), similar to the MAE but which penalises large errors more heavily due to squaring.
To compare the two measures MAE asks: "how far off were people usually?" and RMSE asks: "how far off were people, especially counting those who were really far off?" For Jar A, RMSE was ~32 sweets. For Jar B, RMSE was ~37 sweets. When RMSE is notably larger than MAE (as it is here), it indicates there are some large outliers.
There we have it. We have illustrated that the results strongly support the wisdom of crowds hypothesis. All collective measures (mean, median, trimmed mean) significantly outperformed average individual estimates for both our samples.
Collective measures showed remarkably low error rates (0.42%-5.00%)
Individual guesses demonstrated high variability (MAE: 23-30 sweets)
Higher RMSE values indicate presence of significant outliers and the trimmed mean performed particularly well, suggesting value in outlier removal.
Correcting Systemic Biases
Inevitably, the question remained: how can I leverage these findings to win the next office sweet jar contest? Would using a measure of central tendency be sufficient to guarantee an ultimate statistical victory?
For my two jars, the trimmed mean performed well, but it is not clear how well this performance generalises to other contexts and whether it represents an optimal aggregation strategy. Although these measures of central tendency empirically demonstrate accuracy in the case of our jars, they do not to address directly the biases that are likely to be the root cause of the margin of error.
For instance, in real-world contexts, it is more common for individuals to share information with, and influence, one another. Indeed, as observed above, it is quite possible that there was some information leakage in our rudimentary test. In such cases, it is likely that the individual estimates used to calculate a collective estimate will be correlated to some degree. Social influence cannot only shrink the distribution of estimates but may also systematically shift the distribution, depending on the rules that individuals follow when updating their personal estimate in response to available social information.
For example, if individuals with extreme opinions are more resistant to social influence, then the distribution of estimates will tend to shift towards these opinions, leading to changes in the collective estimate as individuals share information with each other. In short, social influence may induce estimation bias, even if individuals in isolation are unbiased.
My next avenue of exploration was to understand the distribution of the guesses better. So I plotted histograms:
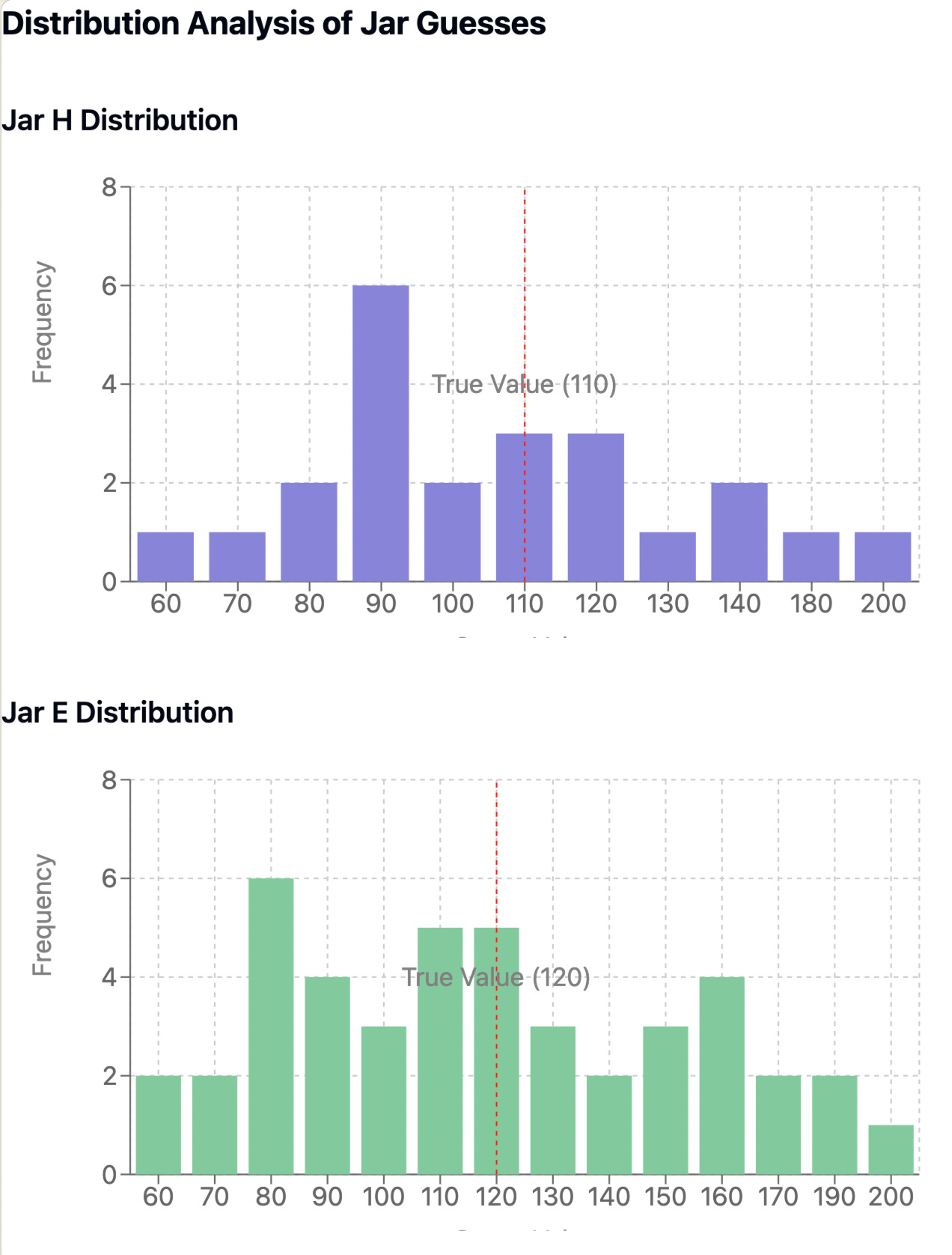
A quick visual assessment confirms that this histogram is not normally distributed. Indeed, even in the summary statistical data, it is clear that there is a hierarchical relationship between the mean, trimmed mean, and median (mean > trimmed mean > median).
This hierarchical relationship indicates that distribution of guesses for both jars exhibits a positive skewness (longer right-hand side tails), suggesting a consistent tendency toward overestimation. I explored these relationships in an earlier piece that can be read here:
Jar A’s distribution is highly positively skewed, with a skewness of 1.33, while Jar B’s distribution is more moderately positively skewed, with a skewness of 0.42. Jar B’s lower skewness is likely explained by the relatively larger size of the sample of guesses. With larger samples, distributions tend to become more symmetric (closer to a normal distribution) as extreme outliers have less impact on the overall shape and the larger sample better represents the true underlying distribution.
The presence of such systematic overestimation bias suggests that simple arithmetic averaging may not be optimal for crowd estimation. In fact, this distribution is indicative of a type of non-normal distribution known as a lognormal distribution where log-transformed data should be more normally distributed.
To confirm the lognormal nature of the guesses, I prepared Q-Q plots to compare the original observed data and log-transformed data against theoretical normal distributions:
The points show some deviation from the reference lines, particularly at the tails, but generally follow a pattern consistent with a lognormal distribution. There's some curvature in the middle section, suggesting that while the data might be approximately lognormal, there might be some departures from this distribution.
A quick search of the web brought up a study that studies this systematic bias pattern, Kao et al. (2018) paper titled, "Counteracting estimation bias and social influence to improve the wisdom of crowds."1
This research paper investigates how individual biases and social influences affect collective estimates in numerosity estimation tasks and uses a sweet jar as its example too. The authors argue that while aggregating non-expert opinions can enhance accuracy, biases can lead to systematic errors in collective estimates. The key biases of concern to the researchers were:
Estimation biases: Kao et al. identify that individual estimates tend to be biased, often leading to overestimation by the arithmetic mean and underestimation by the median. They highlight that these biases can be quantified and mapped to collective biases.2
Social influence biases: The paper also explores how social information sharing impacts individual estimates. They conducted experiments to quantify the rules of social influence, revealing that individuals are more likely to adjust their estimates when social information is higher than their own. Experiment details provided in footnote.3
The authors propose three new aggregation methods that should effectively counteract estimation biases and social influences. These include a corrected mean, a corrected median, and a maximum-likelihood estimate method, all designed to improve collective accuracy.
Let’s consider their proposed maximum likelihood aggregation measure. For this, the Kao et al. model assumes that for a true jar count J:
The log of estimates follows a normal distribution
The mean (μ) of this distribution = 0.87 * ln(J) + 0.68
The standard deviation (σ) = 0.16 * ln(J) - 0.30
Applying this to the data for Jar B data, I did the following:
Calculated the expected μ and σ using above formulas and, given the similarity of the tasks (sweet jars vs. jellybean jars). Assumed the same parameters, namely:
m_μ = 0.87 # slope for mu
b_μ = 0.68 # intercept for mu
m_σ = 0.16 # slope for sigma
b_σ = -0.30 # intercept for sigma
Computed how likely each observed estimate would be under this distribution (the log likelihood).
Summed the log likelihoods to get total likelihood for the Jar.
This analysis returned a total log likelihood of -16.43, which implied a maximum likelihood ~119.5 versus a true value of 120.
In summary, our rudimentary sweet jar experiment provides a real-world demonstration of both crowd wisdom and its inherent biases, while showing how statistical methods can improve crowd estimation accuracy.
The fact that both the mean and median worked well as estimators without correcting for bias is a remarkable testament to the wisdom of crowds effect. It suggests that even with systematic bias present, the aggregate wisdom still manages to cut through to something akin to the truth.
Galton & the Ox
Having satisfied my initial curiosity, it then occurred to me that this hypothesis must have undergone extensive testing in more rigorous, scientific contexts prior to my foray above especially given that the “the wisdom of crowds” effect seemed to be well established. Indeed, we have already explored Kao et. al’s intervention.
So, turning briefly to academic literature on crowd estimation behaviour, I identified these studies as being noteworthy:
On collective intelligence: An influential work is Surowiecki's (2004) "The Wisdom of Crowds", subtitled “Why the many are smarter than the few and how collective wisdom shapes business, economies, societies, and nations.” This book provides a theoretical foundation for the study of the collective intelligence that emerges when diverse, independent judgements are aggregated. It examines three types of problems (cognition, coordination, and cooperation) through theoretical frameworks and case studies while demonstrating the broad impact of crowd wisdom on daily life and future possibilities.4
On non-human animals & swarm intelligence: Building on this, Krause et al. (2010) documented how swarm intelligence manifests in both human and animal groups, offering insights into collective estimation behaviour. Swarm intelligence is the phenomenon where collectives can solve complex problems beyond individual capabilities. Animals, birds and insects, offer a multitude of examples of complex adaptive systems at work and demonstrate how collectives can function effectively without leaders. Influential papers on this theme explore fish shoals, flocks of birds, bee hives, and ant colonies.5 It also transpires that Kao runs a lab at the University of Massachusetts Biology Department that studies collective decision-making in animal groups. The About Us page for The Kao Lab observes that: “Collective decision-making abounds everywhere in nature and includes dynamics within a cell, the output of a brain, consensus among birds in a flock, and democratic governments.”
On biases relevant to sweet jar estimation: See studies examining the cognitive aspects of quantity estimation. Kaufman et al.'s (1949) classic work on visual number discrimination revealed systematic patterns in how people process numerical estimates, including the tendency to favour certain numbers. Raghubir and Krishna (1999) specifically investigated container-based estimation, demonstrating how factors like transparency and shape significantly influence quantity perception.6
Besides these eminent studies, I was particularly impressed by an early example of a wisdom of crowds experiment published by Francis Galton (1907).
This is Francis’ second appearance on the blog, the first can be found here:
As regular readers will recall, Francis Galton was a Victorian-era polymath (and half-cousin of Charles Darwin). Galton’s legacy is controversial due to his role in pioneering statistical methods while simultaneously advocating for theories of eugenics.
While attending the West of England Fat Stock and Poultry Exhibition in Plymouth in 1906, Galton came across a competition where locals competed to guess the weight of an ox. As a statistician interested in human measurement and variation, Galton thought he had identified an opportunity to test a hypothesis about the intellectual capacity of people of lower social status.

In a piece titled ‘Vox Populi’ published in Nature, the scientific journal, Galton described his methodology:
A weight-judging competition was carried on at the annual show of the ‘West of England Fat Stock and Poultry Exhibition’ recently held at Plymouth.
A fat ox having been selected, competitors bought stamped and numbered cards, for 6d. each, on which to inscribe their respective names, addresses, and estimates of what the ox would weigh after it had been slaughtered and dressed. Those who guessed most successfully received prizes.
About 800 tickets were issued, which were kindly lent me for examination after they had fulfilled their immediate purpose. These afforded excellent material.
The judgments were unbiased by passion and uninfluenced by oratory and the like. The sixpenny fee deterred practical joking, and the hope of a prize and the joy of competition prompted each competitor to do his best. The competitors included butchers and farmers, some of whom were highly expert in judging the weight of cattle; others were probably guided by such information as they might pick up, and by their own fancies.
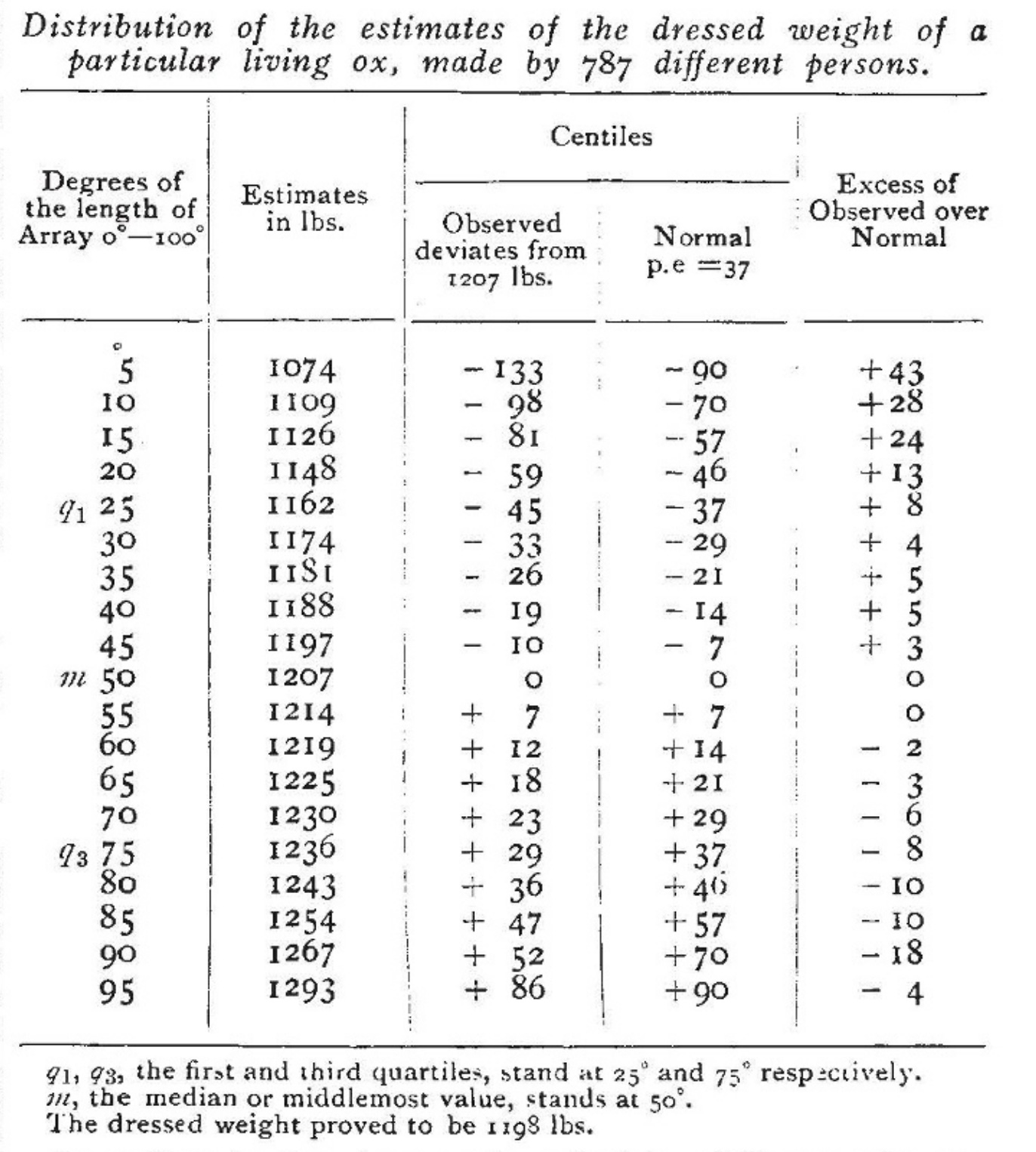
After weeding thirteen cards out of the collection, as defective or illegible, there remained 787 for discussion. I arrayed them in order of the magnitudes of the estimates. Table of data (see footnote).7
Francis Galton, Vox Populi, Nature 75, 450–451 (1907)
After the competition, Galton acquired all the tickets. Galton had hypothesised that the crowd, mostly comprising ordinary citizens with no expertise in livestock, would be far off in their guesses. This hypothesis would likely have been based on his pre-existing belief in the genetic superiority of elite classes.
Instead, to his great surprise, Galton discovered that the median guess was remarkably accurate. Despite his enduring belief in hereditary intelligence and class hierarchy, his experiment had inadvertently identified the wisdom of crowds through pure scientific curiosity.
It appears then, in this particular instance, that the vox populi is correct to within 1 per cent of the real value, and that the individual estimates are abnormally distributed in such a way that it is an equal chance whether one of them, selected at random, falls within or without the limits of -3.7 per cent and +2.4 per cent of their middlemost value.
Galton (1907)
It is worth noting that Galton did not attempt to doctor the experiment, data, or results to match his own beliefs. Rather, he presented the data as it appeared. Moreover, he seems to have updated his priors in light of the new evidence, concluding as follows:
This result is, I think, more creditable to the trustworthiness of a democratic judgment than might have been expected
The average competitor was probably as well fitted for making a just estimate of the dressed weight of the ox, as an average voter is of judging the merits of most political issues on which he votes, and the variety among the voters to judge justly was probably much the same in either case.
Galton (1907)
In a follow-up paper, Galton advocates for the median rather than the mean average as the preferred measure of central tendency. Galton thought that this measure better mitigated the influence of "'cranks in proportion to their crankiness”.8
Closing Remarks: Sweet Jars & Financial Markets
At this point, I realise that what began as a tongue-in-cheek analysis has ballooned into something altogether larger. It has, quite frankly, all got rather out of hand and we are now very deep in the rabbit hole.
It occurs to me that this line of inquiry could be developed further with reference to a broad variety of concepts. Above all, this analysis is relevant to several concepts that are now well-established in finance, and particularly behavioural finance.
Investing, after all, is all about estimating value based on imperfect information, while markets are prediction and betting aggregators. Valuing a financial asset is, in some sense, just like guessing the number of sweets in the jar. Therefore, as an investor, it is worth knowing as much as we can about how to be good at making predictions and the limits of individual and collective human forecasting ability.
Next time, I intend to explore some of the applications of the wisdom of crowds beyond the bounds of sweet jars.
Thank you for reading. As always, feel free to reply if you have comments, questions or suggestions.
Reader Follow-ups
One reader pointed out that the wisdom of crowds hypothesis has been proven many times via the ‘ask the audience’ segment of ‘Who wants to be a Millionaire?’ A quick search online suggests that, after 15 years of the show, the 'ask the audience' success rate is between 91% and 92%, compared to a 66% success rate for the 'phone a friend.'
What was the gender breakdown of participants? Across the two jars, 49% of guesses were submitted by participants who identified as female (33 of 67 total guesses).
What was your guess? I participated in Jar B, my guess was 118 a versus true value of 120… (!)
Kao AB, Berdahl AM, Hartnett AT, Lutz MJ, Bak-Coleman JB, Ioannou CC, Giam X, Couzin ID. (2018) “Counteracting estimation bias and social influence to improve the wisdom of crowds”. J. R. Soc. Interface 15: 20180130. Free version.
Each participant was presented with one jar containing one of the following numbers of objects: 54 (n = 36), 139 (n = 51), 659 (n = 602), 5897 (n = 69) or 27,852 (n = 54) (see figure 1a for a representative photograph of the kind of object and jar used for the three smallest numerosities; electronic supplementary material, figure S1 for a representative photograph of the kind of object and jar used for the largest two numerosities.). To motivate accurate estimates, the participants were informed that the estimate closest to the true value for each jar would earn a monetary prize. The participants then estimated the number of objects in the jar. No time limit was set, and participants were advised not to communicate with each other after completing the task.
The participants first recorded their initial estimate, G1. Next, participants were given ‘social’ information, in which they were told that N = {1, 2, 5, 10, 50, 100} previous participants’ estimates were randomly selected and that the ‘average’ of these guesses, S, was displayed on a computer screen. Unbeknownst to the participant, this social information was artificially generated by the computer, allowing us to control, and thus decouple, the perceived social group size and social distance relative to the participant’s initial guess. Half of the participants were randomly assigned to receive social information drawn from a uniform distribution from G1/2 to G1, and the other half received social information drawn from a uniform distribution from G1 to 2G1. Participants were then given the option to revise their initial guess by making a second estimate, G2, based on their personal estimate and the perceived social information that they were given. Participants were informed that only the second guess would count towards winning a monetary prize. We therefore controlled the social group size by varying N and controlled the social distance independently of the participant’s accuracy by choosing S from G1/2 to 2G1.
Surowiecki, J. (2004). The wisdom of crowds: Why the many are smarter than the few and how collective wisdom shapes business, economies, societies, and nations. Doubleday & Co.
Krause, J., Ruxton, G. D., & Krause, S. (2010). "Swarm intelligence in animals and humans." Trends in Ecology & Evolution, 25(1), 28-34.
Ioannou CC. 2017 “Swarm intelligence in fish? The difficulty in demonstrating distributed and self-organised collective intelligence in (some) animal groups.” Behav. Processes 141, 141 –151.
Sumpter D, Krause J, James R, Couzin I, Ward A. 2008 “Consensus decision making by fish.” Curr. Biol.18, 1773–1777.
Sasaki T, Granovskiy B, Mann R, Sumpter D, Pratt S. 2013 “Ant colonies outperform individuals when a sensory discrimination task is difficult but not when it is easy.” Proc. Natl Acad. Sci. USA 110, 13 769–13 773.
Sasaki T, Pratt S. 2011 “Emergence of grouprationality from irrational individuals.” Behav. Ecol. 22, 276–281.
Tamm S. 1980 “Bird orientation: single homing pigeons compared to small flocks.” Behav. Ecol. Sociobiol. 7, 319– 322.
Berdahl AM, Kao AB, Flack A, Westley PAH, Codling EA, Couzin ID, Dell AI, Biro D (2018) “Collective animal navigation and the emergence of migratory culture.” Philosophical Transactions of the Royal Society: B 373(1746):20170009.
Kaufman, E. L., Lord, M. W., Reese, T. W., & Volkmann, J. (1949). "The discrimination of visual number." The American Journal of Psychology, 62(4), 498-525.
Raghubir, P., & Krishna, A. (1999). "Vital dimensions in volume perception: Can the eye fool the stomach?" Journal of Marketing Research, 36(3), 313-326.
Krueger LE. 1984 “Perceived numerosity: a comparison of magnitude production, magnitude estimation, and discrimination judgements.” Atten. Percept. Psychophys.35, 536–542.